Class 10 Mathematics Chapter 2| বহুপদ |SEBA: আমাৰ ৱেবছাইটলৈ স্বাগতম! আপোনাৰ শৈক্ষিক যাত্ৰাৰ বাবে আপোনাক দশম শ্ৰেণীৰ Notes প্ৰদান কৰি আমি আনন্দিত।
দশম শ্ৰেণী শিক্ষাৰ্থীসকলৰ বাবে এক গুৰুত্বপূৰ্ণ বছৰ কিয়নো তেওঁলোকে আগন্তুক ব’ৰ্ড পৰীক্ষাৰ বাবে নিজকে প্ৰস্তুত কৰে, যি তেওঁলোকৰ শৈক্ষিক সফলতা নিৰ্ধাৰণ কৰিব।
আজি, এই পাঠটোৰ মই দশম শ্ৰেণীৰ “বহুপদ ” দীঘলয়া আৰু চুটি প্ৰশ্ন আলোচনা কৰিম| আমি প্ৰায় সকলো দীঘলয়া আৰু চুটি প্ৰশ্ন Solution প্ৰদান কৰিছোঁ।
আমাৰ লক্ষ্য হৈছে আপোনাৰ প্ৰয়োজনীয়তা পূৰণ কৰা। আমি ইয়াত বিনামূলীয়াকৈ Notes সমূহ প্ৰদান কৰিছো। আমি আপোনাক আগন্তুক পৰীক্ষাৰ বাবে শুভেচ্ছা জনাইছো। যদি আপোনাৰ কোনো সন্দেহ আছে তেন্তে আমাৰ সৈতে যোগাযোগ কৰক।
Class 10 Mathematics Chapter 2 Question Answer:
পাঠভিত্তিক প্রশ্নোত্তৰ
অনুশীলনী-2.1
1. কিছুমান বহুপদ p(x) অৰ ক্ষেত্ৰত y = p(x) ৰ লেখবোৰ তলৰ চিত্ৰত দিয়া আছে। প্ৰতিটো ক্ষেত্ৰতে p(x)ৰ শূন্যৰ সংখ্যা উলিওৱা ।
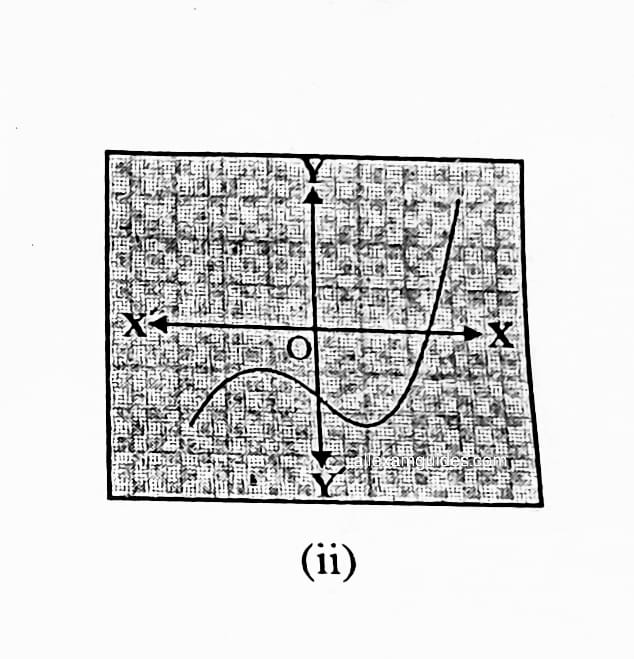
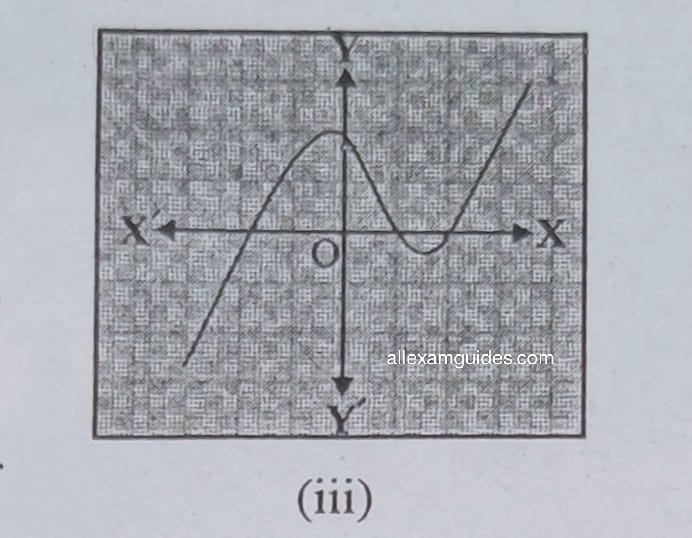
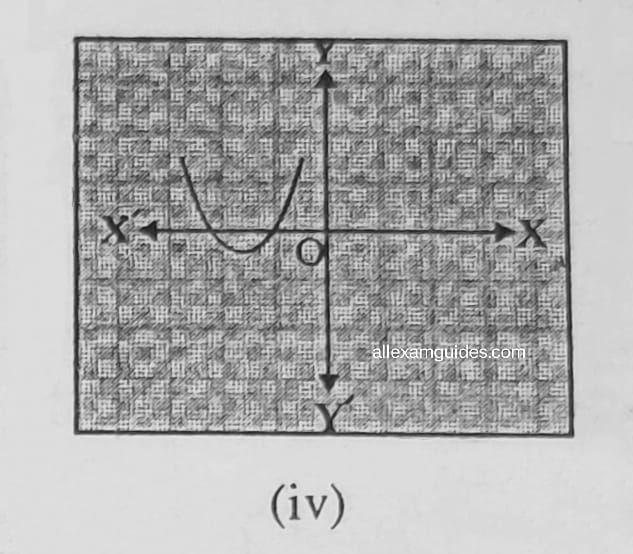
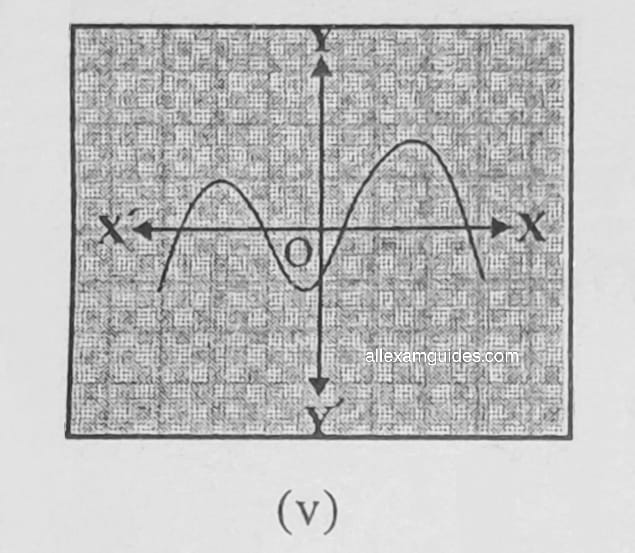
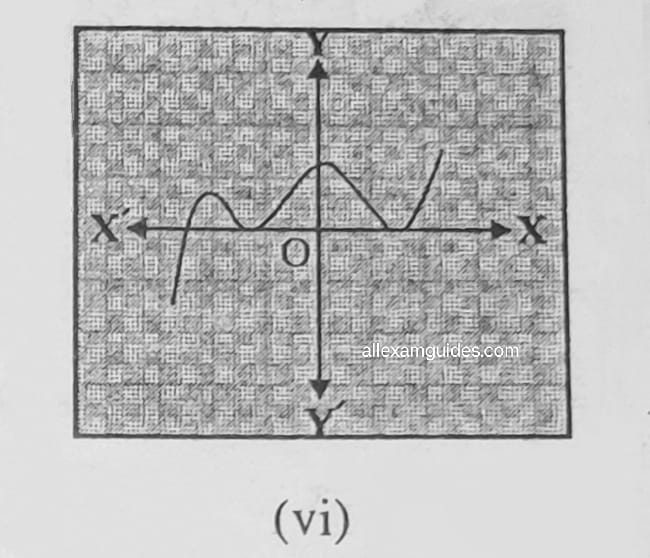
সমাধানঃ (i) শূন্য নাই (ii) 1, (iii) 3, (iv) 2, (v) 4, (vi) 3
অনুশীলনী-2.2
1. তলৰ দ্বিঘাত বহুপদবোৰৰ শূন্য উলিওৱা আৰু এই শূন্যবোৰ আৰু সহগবোৰৰ মাজৰ সম্পৰ্ক সত্যাপন কৰা।
(i) x²- 2x – 8 (ii) 4s² – 4s + 1 (iii) 6x2 – 3 – 7x [HSLC 2017]
(iv) 4u – 8u (v) t – 15 (vi) 3x2 – x–4
সমাধানঃ (i) x2–2x-8 = x2 – 4x + 2x = 8
= x(x – 4) + 2(x – 4) = (x + 2) (x – 4 )
শূন্য দুটা –2 আৰু 4.
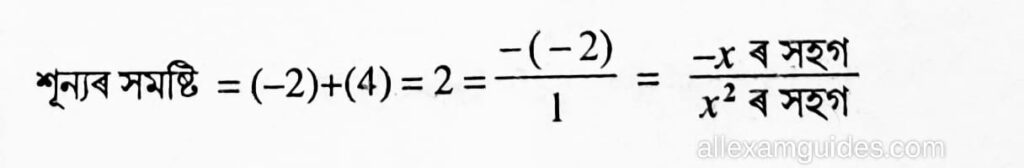
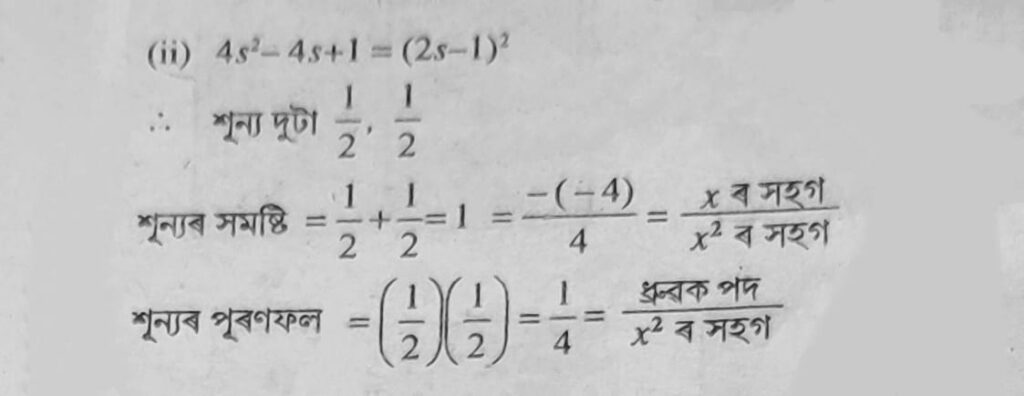


(v) t2 – 15 = t2(√15)2 = (t+√15)(t-√15)
p(t) = t2 + 0t– 15 ৰ শূন্য দুটা – √15 আৰু √15.
শূন্যৰ সমষ্টি = (– √15) + √15 = 0 = -t ৰ সহগ/t2 ৰ সহগ
শূন্যৰ পুণফল = (– √15)×(√15) = -15 (–15)/1 = ধ্রুৱক পদ/t2 ৰ সহগ

2. তলৰ যোৰকেইটাৰ সংখ্যা দুটাক ক্ৰমে শূন্যবোৰৰ সমষ্টি আৰু গুণফল হিচাপে ধৰি প্ৰত্যেকৰ ক্ষেত্ৰত একোটা দ্বিঘাত বহুপদ নিৰ্ণয় কৰা।
(i) 1/4,-1 (ii) √2, 1/3 (iii) 0, √5
(iv) 1, 1 (v)1/4 , 1/4 (vi) 4, 1
সমাধানঃ ধৰাহ’ল বহুপদটো ax2 + bx + c আৰু ইয়াৰ শূন্য দুটা α আৰু β
(i) ইয়াত , α + β আৰু αβ = – 1
গতিকে বহুপদটো = x2 – (শূন্যৰ সমষ্টি)x + শূন্যৰ পূৰণফল
= x2 (1/4)x – 1 বা x2 – x/4 – 1
আন বহুপদটো k( x2 – x/4 – 1 )
যদি k = 4 হয়, তেতিয়া বহুপদটো 4x2 – x – 4
(ii) ইয়াত, α x β =√2 αβ=1/3
গতিকে বহুপদটো = x2 – (শূন্যৰ সমষ্টি)x + শূন্যৰ পূৰণফল
= x2 (√2)x + 1/3 বা x2 – √2x + 1/3
আন বহুপদটো k(x2 + √2x + 1/3)
যদি k = 3 হয়, তেতিয়া বহুপদটো 3x2– 3√2x + 1
(iii) ইয়াত, α + β = 0 আৰু αβ = √5
গতিকে বহুপদটো = x2 – (শূন্যৰ সমষ্টি)x + শূন্যৰ পূৰণফল
= x2–(0)x+√5 = x+√5
(iv) ইয়াত α + β = 1 , αβ = 1
গতিকে বহুপদটো = x2 – (শূন্যৰ সমষ্টি)x + শূন্যৰ পূৰণফল
= x2 –(1)x+1= x2 -x+1
(v) ইয়াত α + β = – 1/4 , αβ = 1/4
গতিকে বহুপদটো = x2 – (শূন্যৰ সমষ্টি) x + শূন্যৰ পুৰণফল
= x2 – (1/4)x + 1/4 = x2 – 1/4 + 1/4
আন বহুপদটো = k( x2 – 1/4x + 1/4 )
যদি k = 4, তেনেহ’লে বহুপদটো = 4x2 + x + 4.
(vi) ইয়াত α + β = 4 , αβ = 1
গতিকে বহুপদটো = x2 – (শূন্যৰ সমষ্টি)x + শূন্যৰ পূৰণফল
= x2 – (4)x+1 = x2 – 4x + 1
3. দ্বিঘাত বহুপদবোৰ নিৰ্ণয় কৰা যাৰ শূন্যকেইটা তলত দিয়া ধৰণৰ :
(i) – 4 আৰু 3/2 [HSLC 2022] (ii) 5 আৰু 2 (iii) 1/3 আৰু -1
(iv) 3/2 আৰু -2
সমাধানঃ (i) ধৰা হ’ল α = 4 আৰু β = 3/2
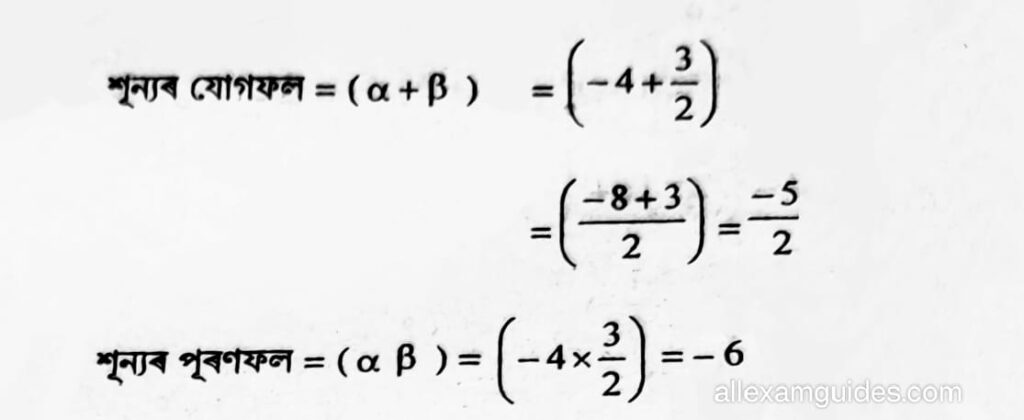
গতিকে দ্বিঘাত বহুপদটো x2 – (α + β ) x + αβ
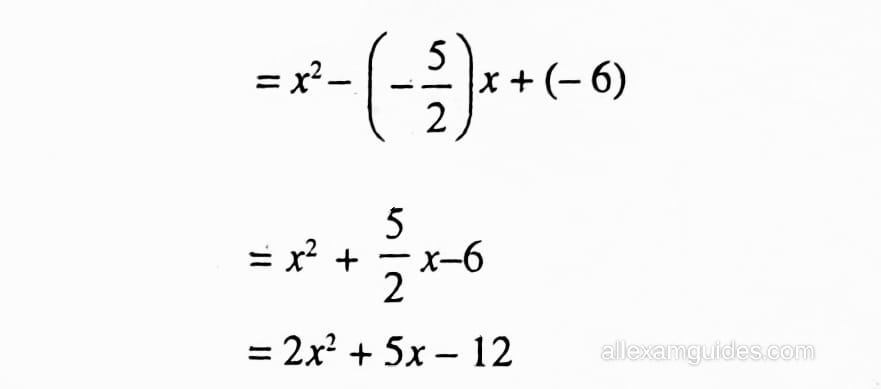
সমাধানঃ (ii) ধৰা হ’ল, α =5 আৰু β =2
শূন্যৰ যোগফল = (α + β) = (5+ 2) = 7
শূন্যৰ পূৰ্ণফল = (αβ) = (5x 2 ) = 10
গতিকে দ্বিঘাত বহুপদটো x2 – (α + β ) x + αβ
= x2 – 7x + 10
সমাধানঃ (iii) ধৰা হ’ল α = 1/3 আৰু β = 1
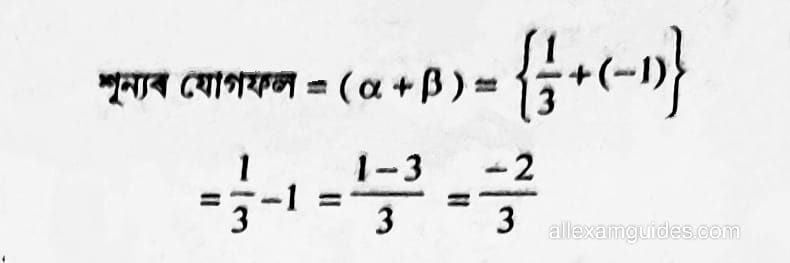
শূন্যৰ পুৰণফল = (αβ) = 1/3 x (-1) = –1/3
গতিকে দ্বিঘাত বহুপদটো = x2 = (α + β) x + αβ
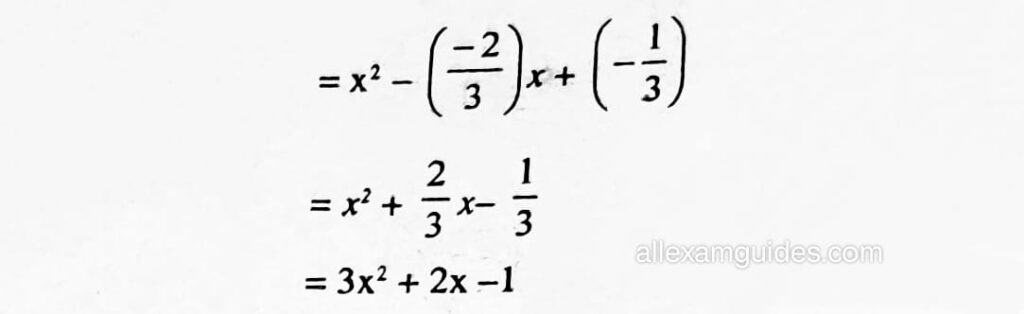
সমাধানঃ (iv) ধৰা হ’ল, α = 2/3 আৰু β = – 2
শূন্যৰ পুৰণফল = (αβ) = 2 ×(–2) = 3
গতিকে দ্বিঘাত বহুপদটো = x2 – (α + β) x + αβ
= x² + 1/2x – 3
= x2– 1/2x – 3
= 2x² + x – 6
অনুশীলনী-2.3
1. p(x) বহুপদটোক g(x) বহুপদটোৰে হৰণ কৰা আৰু প্ৰতিটোৰে ক্ষেত্ৰত ভাগফল আৰু ভাগশেষ নির্ণয় কৰা:
(i) p (x) = x3 – 3x2 + 5x – 3, g(x) = x2 – 2 [HSLC 2019]
(ii) p (x) = x4-3x2 + 4x + 5, g(x) = x2 + 1 – x
(iii) p (x) = x4 – 5x + 6, g(x) = 2 – x2 [HSLC 2020]
(iv) p(x) = 2x4 + 2x3 – 2x2 – 9x – 12 g(x) = x2 – 3
(v) p (x) = x6 + 3x2 + 10 g(x) = x2 + 1
(vi) p(x) = 2x5 – 5x4 + 7x3 + 4x2 – 10x2 – 11 g(x) = 2 – x2
সমাধানঃ
(i)
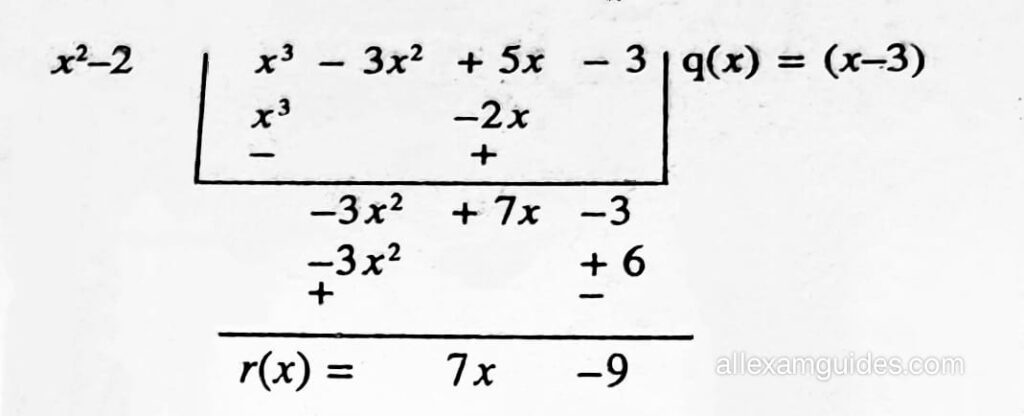
গতিকে, ভাগফল q(x) = x − 3 আৰু ভাগশেষ r(x) =7x- 9
(ii)
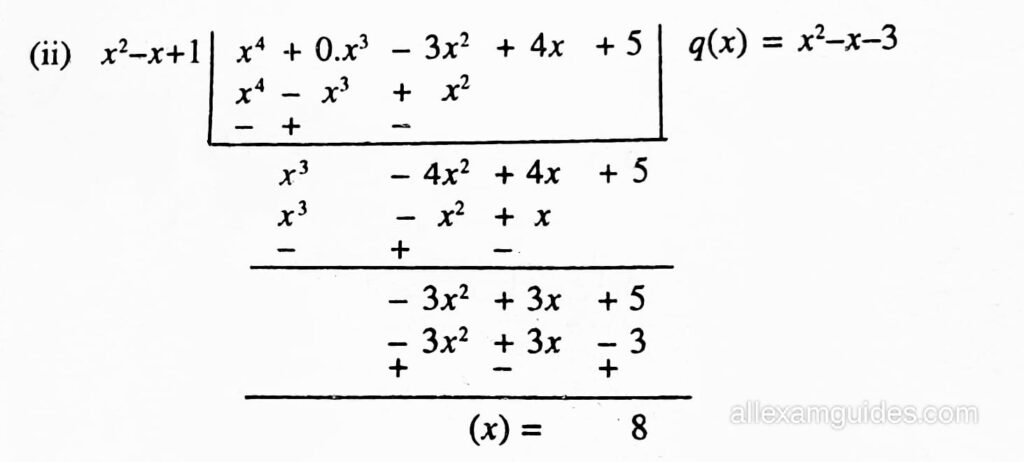
গতিকে, ভাগফল = x2 + x – 3, ভাগশেষ = ৪
(iii)
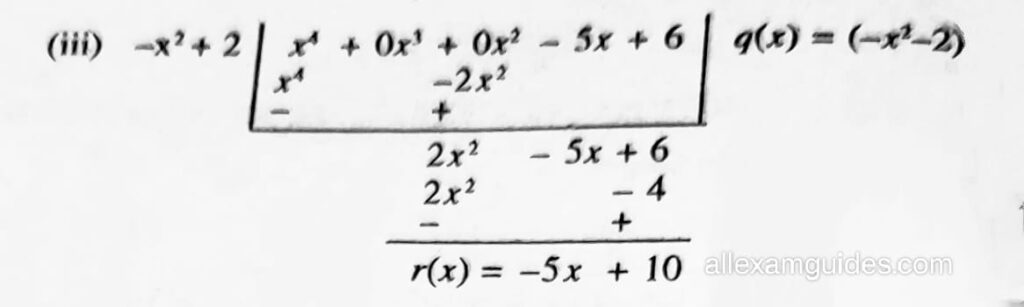
গতিকে, ভাগফল = x2-2 আৰু ভাগশেষ (−5x +10).
সমাধানঃ (iv)

সমাধানঃ (v) P(x) = x6 + 3x2 + 10
q(x) = x3 + 1
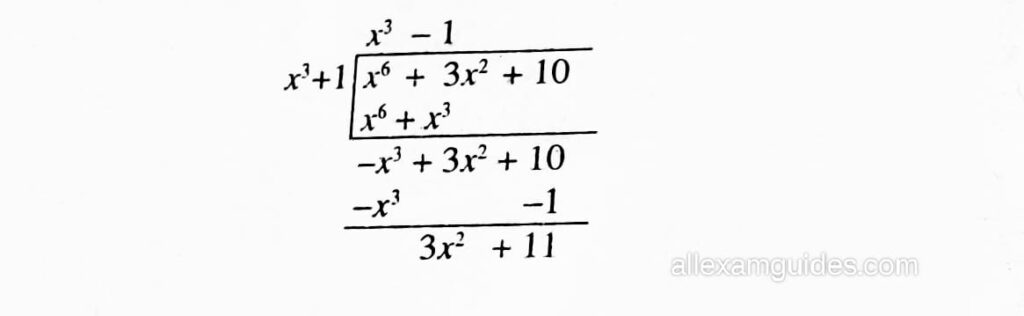
:. ভাগফলq (x) = x-1
ভাগশেষ r(x) = 3x2+11
সমাধানঃ (vi) P(x) = 2x5 -5x4 + 7x3 + 4x2 – 10x + 11
q(x) = x2 + 2
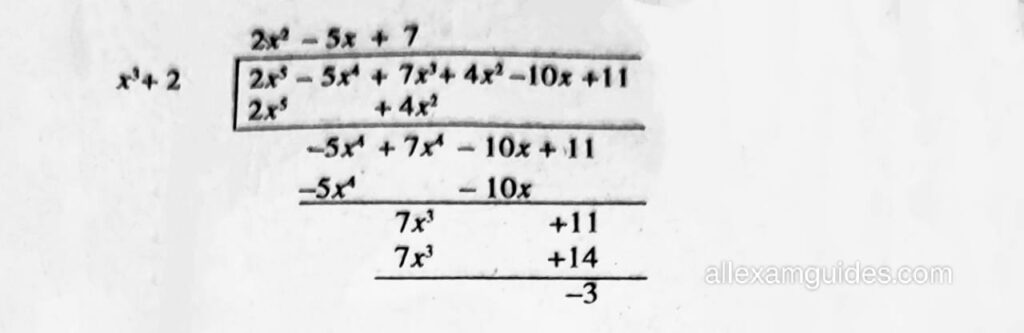
ভাগফল q(x) = 2x2-5x + 7
ভাগশেষ r(x) = – 3
2. দ্বিতীয় বহুপদটোক প্রথম বহুপদেৰে হৰণ কৰি প্ৰথম বহুপদটো দ্বিতীয় বহুপদটোৰ এটা উৎপাদক হয়নে নহয় পৰীক্ষা কৰা:
(i) t²-3, 2t4+3t3-2t2– 9t – 12
(ii) x2 + 3x + 1, 3x4 + 5x3-7x2 + 2x + 2
(iii) x3 -3x + 1, x5 − 4x3 + x2 + 3x + 1
সমাধানঃ (i)

গতিকে, t2–3, 2r4 + 3t3 – 2t2 -9t –12 ৰ এটা উৎপাদক।
সমাধানঃ (ii)

গতিকে, x2 + 3x+1 ৰে 3x4+5x3-7x2 + 2x + 2 বহুপদটোক বিভাজ্য হয়।
সমাধানঃ (iii)
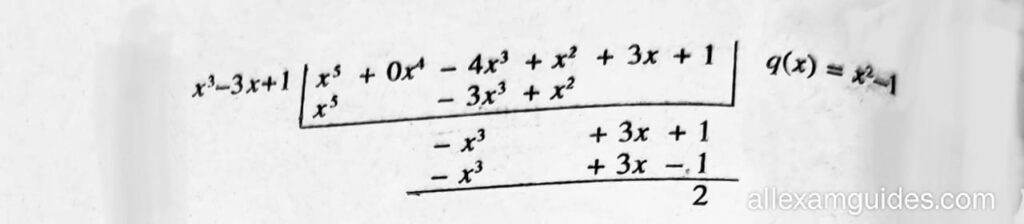
ইয়াত, ভাগশেষ = 20.
গতিকে, x3-3x + 1 ৰে x5-4x3 + x2 + 3x + 1 বহুপদটোক বিভাজ্য নহয়।
3. যদি দুটা শূন্য √(5/3) আৰু -√(5/3) তেন্তে 3x4 + 6x3 – 2x2 – 10x – 5 ৰ বাকী আটাইবোৰ শূন্য উলিওৱা।
সমাধানঃ 3x4 + 6x3– 2x2 – 10x – 5ৰ শূন্য দুটা √(5/3) আৰু -√(5/3)
x = √(5/3), x= -√(5/3) ⇒ (x -√(5/3)) (x + √(5/3)) = x2 + √(5/3) বা 3x2 – 5 প্রদত্ত বহুপদটোৰ উৎপাদক।
এতিয়া,
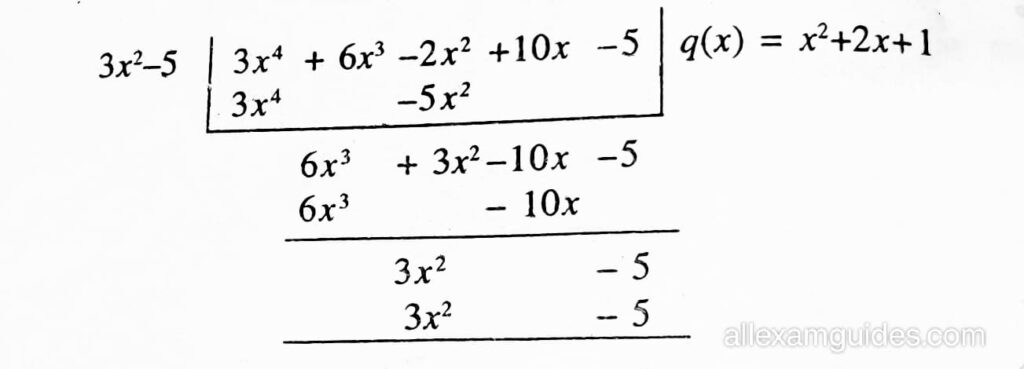
এতিয়া, x2+2x+1 = (x+1)2
ইয়াৰ শূন্য –1, −1,গতিকে, আন শূন্য দুটা −1, −1
4. 4x3 – 3x2 + x + 2 ক এটা বহুপদ g(x)ৰে হৰণ কৰাত ভাগফল x – 2 আৰু ভাগশেষ – 2x + 4 পোৱা গ’ল। g(x) উলিওৱা।
সমাধানঃ x3 – 3x2 + x + 2 = g(x) × (x – 2) + (-2x+4)
⇒ g (x) × (x – 2) = {x3– 3x2+x+2} -{-2x+4}
⇒ g(x) × (x – 2) = x3-3x2+3x-2}
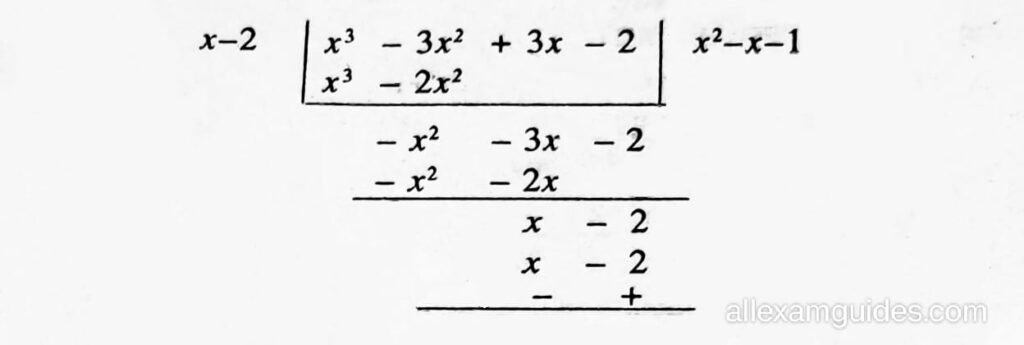
গতিকে, x3–3x2 + 3x – 2 = (x – 2) × ( x2 – x + 1)
(1) আৰু (2) ৰ পৰা আমি পাওঁ, g(x) × (x – 2) = (x2-x+1) × (x-2) ⇒ g(x)= x2 – x + 1
5. কেইটামান বহুপদ p (x), g (x), q(x) আৰু r(x)ৰ উদাহৰণ দিয়া যাতে ইহঁতে বিভাজন কলনবিধি সিদ্ধ কৰে আৰু
(i) p(x)ৰ মাত্ৰা = q (x) ৰ মাত্ৰা
(ii) q (x) ৰ মাত্ৰা = r(x)ৰ মাত্ৰা
(iii) r(x)ৰ মাত্ৰা = 0
সমাধানঃ (i)
q(x) = 3x2 + 2x + 6, q (x) ৰ মাত্রা = 2
p (x) = 12x2 + 8 x + 24, p (x) ৰ মাত্ৰা = 2
গতিকে, p(x) ৰ মাত্ৰা = q(x) ৰ মাত্ৰা।
(ii) p (x) = 2x2 + 2x + 8
q(x) = x2 + x + 9
q(x) = 2; r(x) = -10
ইয়াত, r(x) ৰ মাত্ৰা = 0
(iii) p(x)= x3+x+5
g (x) = x2 + 1
g(x) = x
r(x) = 5
ইয়াত, g(x) ৰ মাত্ৰা = r(x) ৰ মাত্ৰা
6. (i) 3x2 – 3x2 + 1 বহুপদটোৰ এটা শূন্য 1। ইয়াৰ বাকীকেইটা শূন্য নির্ণয় কৰা।
(ii) x + x – 9×2 – 3x + 18 বহুপদ দুটাৰ শূন্য √3 আৰু বাকীকেইটা শূন্য নির্ণয় কৰা।
(iii) x + 2×2 – 26×2-54x-27 বহুপদটোৰ দুটা শূন্য 3/3 আৰু ইয়াৰ বাককেইটা শূন্য নিৰ্ণয় কৰা।
সমাধানঃ (i) ধৰা হ’ল P(x) = 3x3 – x2 – 3x + 1
1. P(x) ৰ এটা শূন্য
গতিকে (x−1), (Px) ৰ এটা উৎপাদক
এতিয়া,
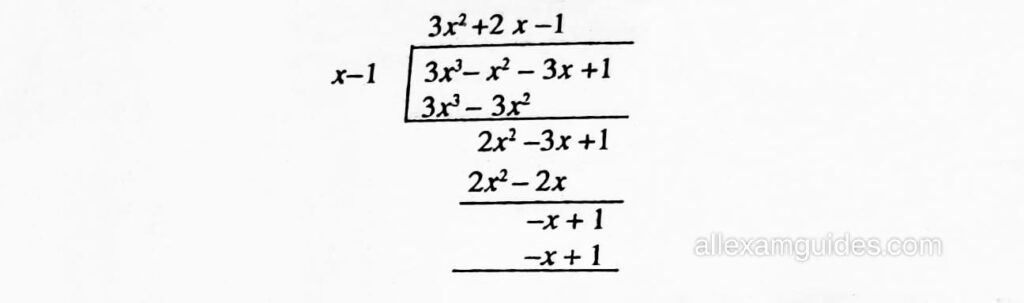
:. P(x) = (3×2 + 2x − 1) (x-1)
= (3x + 3x – x -1) (x-1)
= (3x (x+1)-1(x+1)} (x-1)
= (x+1) (3x-1) (x-1)
:. বাকী শূন্য কেইটা (x+1) = 0 ⇒ x=-1
আৰু 3x−1 = 0 ⇒ x = 1/3
সমাধানঃ (ii) ধৰা হ’ল P(x) = x4+x3-9x2-3x+18
যিহেতু P(x) ৰ শূন্য দুটা √3 আৰু –√3,
গতিকে (x − √3) আৰু (x +√3), P(x) ৰ শূন্য।
অর্থাৎ (x-√3) (x+√3)=x2−3, P(x) ৰ উৎপাদক
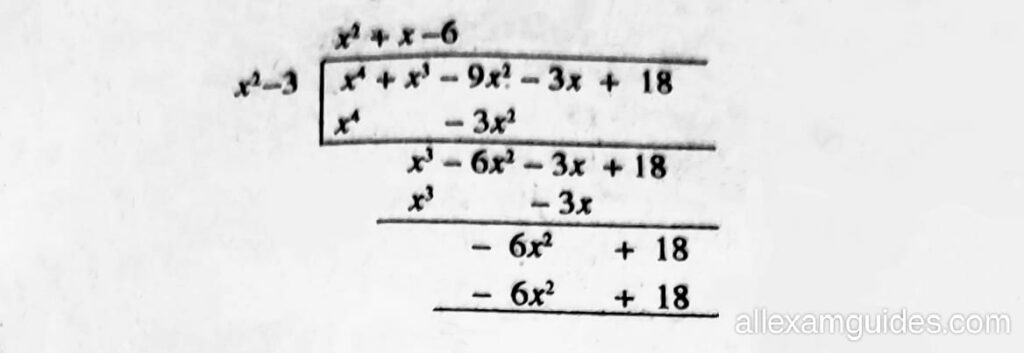
:. P(x) = (x²-3) (x²+x-6)
= (x2 – 3 ) ( x2 + 3x – 2x – 6)
= (x²-3) (x(x + 3)-2 (x-3)} = (x²-3) (x+3)(x-2)
বাকী শূন্য দুটা x+3 = 0 ⇒ x= – 3
আৰু x – 2 = 0 ⇒ x = 2
সমাধানঃ
(iii) ধৰা হ’ল P(x) = x4+2x3 – 26x2-54x – 27
P(x) ৰ শূন্য দুটা আৰু – 3√3.
গতিকে (x-3√3 ) আৰু (x+3√3), P(x) ৰ উৎপাদক। অর্থাৎ (x − 3√3) (x2-27 )P(x) ৰ উৎপাদক।
এতিয়া,
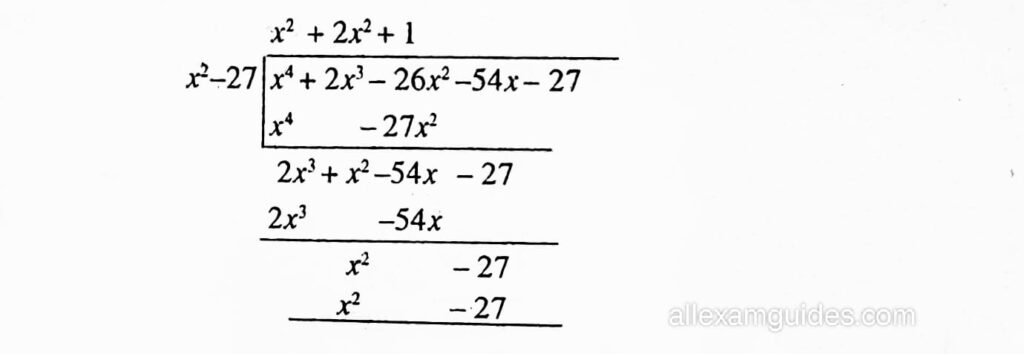
:. P(x) = (x2-27) (x2+2x+1)
= (x²-27) (x+1) (x+1)
:. বাকী শূন্যকেইটা –1 আৰু – 1
7. (i) 6x4-11x3 – 7x2 – 15x – 50 বহুপদটোক আন এটা বহুপদ 3x+7 ৰে হৰণ কৰাত ভাগশেষ – 15 পোৱা গ’ল। ভাগফল কি?
(ii) এটা বহুপদক x2 – 2 ৰে ভাগ কৰাত ভাগফল আৰু ভাগশেষ ক্ৰমে 2x2+5x- 2 আৰু –x + 14 পোৱা গ’ল ৷ বহুপদটো নিৰ্ণয় কৰা।
সমাধানঃ (i) ধৰা হ’ল, P(x) = 6x4+11x3-7x2 – 15x- 50
g(x) = 3x + 7
r (x) = 15
আমি জানো যে, P(x) = g(x) × q(x) + r(x)
⇒ 6x4+11x³-7x²-15x-50= (3x+7) x g(x) + (-15)
⇒ 6x4+11x3-7x2-15x-35 = ( 3 x +7) x q(x)
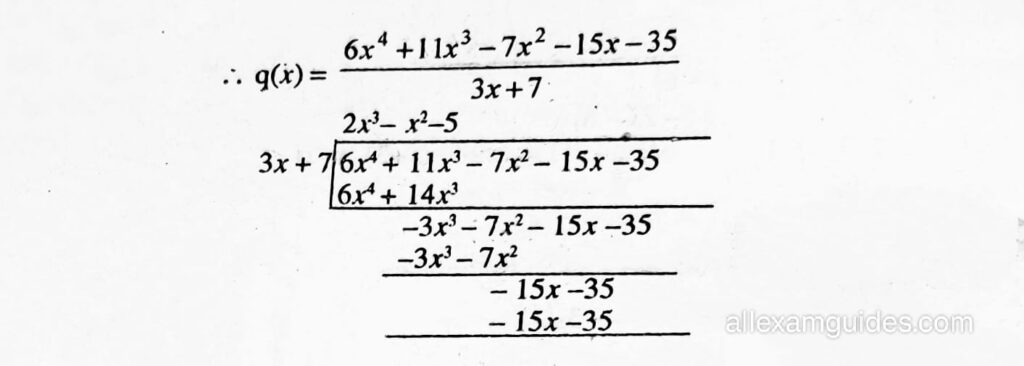
:. q(x) = 2x3 – x2-5
সমাধানঃ (ii) ধৰা হ’ল, ভাজক g(x) = x2 – 2
ভাগফল q(x) = 2x2 + 5x – 2
ভাগশেষ r(x) = x + 14
ভাজ্য P(x) নির্ণয় কৰিব লাগে।
. P(x) = q (x) x q(x) + r (x)
= (x²-2) (2x² + 5x-2) + (-x+14)
= x2 (2x2 + 5x-2) – 2 (2x2 + 5x – 2) – x + 14
=2x4 + 5x3 – 2x2 – 4x2 – 10x + 4 x + 14
=2x4 + 5x3 – 6x2 – 11x – 18
অতিৰিক্ত প্রশ্নোত্তৰ
…………….
Conclusion:
আমি বিশ্বাস কৰোঁ যে এই টোকাবোৰে শিক্ষাৰ্থীসকলক বিষয়বোৰৰ বিষয়ে ভালদৰে বুজাবুজি বিকশিত কৰাত আৰু তেওঁলোকৰ পৰীক্ষাৰ বাবে তেওঁলোকৰ আত্মবিশ্বাস বৃদ্ধি কৰাত সহায় কৰিব।
আমি নিশ্চিত যে এই টোকাবোৰে শিক্ষাৰ্থীসকলক তেওঁলোকৰ লক্ষ্য প্ৰাপ্ত কৰাত আৰু তেওঁলোকৰ শৈক্ষিক প্ৰদৰ্শন বৃদ্ধি কৰাত সহায় কৰিব। যদি আপুনি এই সমাধান সমূহ ভাল পায় আৰু সহায়ক হয় তেন্তে আপোনাৰ বন্ধুবৰ্গৰ সৈতে Share কৰিবলৈ নাপাহৰিব।