Class 10 Mathematics Chapter 1 |বাস্তৱ সংখ্যা |Question Answer | SEBA

Class 10 Mathematics Chapter 1| বাস্তৱ সংখ্যা |SEBA: আমাৰ ৱেবছাইটলৈ স্বাগতম! আপোনাৰ শৈক্ষিক যাত্ৰাৰ বাবে আপোনাক দশম শ্ৰেণীৰ Notes প্ৰদান কৰি আমি আনন্দিত।

দশম শ্ৰেণী শিক্ষাৰ্থীসকলৰ বাবে এক গুৰুত্বপূৰ্ণ বছৰ কিয়নো তেওঁলোকে আগন্তুক ব’ৰ্ড পৰীক্ষাৰ বাবে নিজকে প্ৰস্তুত কৰে, যি তেওঁলোকৰ শৈক্ষিক সফলতা নিৰ্ধাৰণ কৰিব।

আজি, এই পাঠটোৰ মই দশম শ্ৰেণীৰ “বাস্তৱ সংখ্যা ” দীঘলয়া আৰু চুটি প্ৰশ্ন আলোচনা কৰিম| আমি প্ৰায় সকলো দীঘলয়া আৰু চুটি প্ৰশ্ন Solution প্ৰদান কৰিছোঁ।

আমাৰ লক্ষ্য হৈছে আপোনাৰ প্ৰয়োজনীয়তা পূৰণ কৰা। আমি ইয়াত বিনামূলীয়াকৈ Notes সমূহ প্ৰদান কৰিছো। আমি আপোনাক আগন্তুক পৰীক্ষাৰ বাবে শুভেচ্ছা জনাইছো। যদি আপোনাৰ কোনো সন্দেহ আছে তেন্তে আমাৰ সৈতে যোগাযোগ কৰক।

পাঠভিত্তিক প্রশ্নোত্তৰ

অনুশীলনী- 1.1

1. ইউক্লিডৰ কলনবিধি ব্যৱহাৰ কৰি গ.সা.উ. উলিওৱা :

(i) 135 আৰু 225 [HSLC 2022] (ii) 196 আৰু 38220

(iii) 867 আৰু 255 (iv) 272 আৰু 1032

(v) 405 আৰু 2520 (vi) 155 আৰু 1385

(vii) 384 আৰু 1296 (viii) 1848 আৰু 3058

সমাধান : (i) যিহেতু 225 135, 225 আৰু 135 ত ইউক্লিডৰ বিভাজন প্ৰমেয়িকা ব্যৱহাৰ কৰি। আমি পাওঁ,

225 = 135×1+90

যিহেতু ভাগশেষ 90 ≠0, গতিকে, আকৌ 135 আৰু 90 ত ইউক্লিডৰ বিভাজন প্ৰমেয়িকা ব্যৱহাৰ কৰি

আমি পাওঁ, 135 = 90 x 1 + 45

আকৌ, ভাগশেষ 45 ≠0, গতিকে 90 আৰু 45 ত ইউক্লিডৰ প্ৰমেয়িকা ব্যৱহাৰ কৰি আমি পাওঁ,

90 = 45×2+0

ইয়াত ভাগশেষ শূন্য হ’ল। গতিকে আমাৰ প্ৰণালীও বন্ধ হ’ব।

যিহেতু এই পর্যায়ত ভাজক 45, গতিকে 225 আৰু 135 ৰ গ. সা. উ. 45

সমাধান : (ii) 196 আৰু 38220 ত ইউক্লিডৰ বিভাজন প্ৰমেয়িকা ব্যৱহাৰ কৰি আমি পাওঁ,

38220 = 196×195+0

ইয়াত ভাগশেষ শূন্য হ’ল। গতিকে আমাৰ প্ৰণালীও বন্ধ হ’ব।

গতিকে 196 আৰু 38220 ৰ গ. সা. উ. 195

অর্থাৎ, গ. সা. উ. (196,38200) = 195

সমাধান : (iii) ইউক্লিডৰ বিভাজন প্রমেয়িকা ব্যৱহাৰ কৰি আমি পাওঁ

867= 255 x 3 + 102

225 আৰু 102 ত ইউক্লিডৰ বিভাজন প্ৰমেয়িকা ব্যৱহাৰ কৰি আমি পাওঁ,

225= 102 X 2 + 51

আকৌ 102 আৰু 51ত ইউক্লিডৰ বিভাজন প্রমেয়িকা ব্যৱহাৰ কৰি আমি পাওঁ

102 = 51 x 2 +0

গ. সা. উ. (867, 255) = 51.

সমাধানঃ (iv) ইউক্লিডৰ প্ৰমেয়িকা ব্যৱহাৰ কৰি পাওঁ

1032= 272 x 3 +216

272 = 216×1+56

216 = 56 x 3 +48

56 = 48 × 1 +8

48 = 8 x 6 + 0

ইয়াত ভাগশেষ শূন্য হ’ল। গতিকে আমাৰ প্ৰণালীও বন্ধ হ’ব ।

গতিকে 272 আৰু 1032 ৰ গ. সা. উ. ৪.

সমাধানঃ (v) ইউক্লিডৰ প্ৰমেয়িকা ব্যৱহাৰ কৰি পাওঁ

2520= 405 x 6 +80

405 = 90 x 5 +45

90 = 45 x 2 +0

ইয়াত ভাগশেষ শূন্য হ’ল ৷ গতিকে আমাৰ প্ৰণালীও বন্ধ হ’ব।

গতিকে 405 আৰু 2520 ৰ গ. সা. উ. 45.

সমাধান : (vi) ইউক্লিডৰ প্ৰমেয়িকা ব্যৱহাৰ কৰি পাওঁ

1385= 155 x 8 + 145

155= 145 x 1 +10

145 = 10 × 14 +5

10 = 5 x 2 + 0

ইয়াত ভাগশেষ শূন্য হ’ল। গতিকে আমাৰ প্ৰণালীও বন্ধ হ’ব।

155 আৰু 1385 ৰ গ. সা. উ. 5.

সমাধানঃ (vii) ইউক্লিডৰ প্ৰমেয়িকা ব্যৱহাৰ কৰি পাওঁ

1296 = 384 x 3 + 144

384 = 144 x 2 + 96

144 = 96 x 1 +48

96 = 48×2+0

ইয়াত ভাগশেষ শূন্য হ’ল। গতিকে আমাৰ প্ৰণালীও বন্ধ হ’ব।

গতিকে, 384 আৰু 1296 ব গ. সা. উ. 48,

সমাধান : (viii) ইউক্লিডৰ প্ৰমেয়িকা ব্যৱহাৰ কৰি পাওঁ

1458 = 1848 × 2 +362

1848 = 362 x 5+38

362 = 38 x 9 + 20

38 = 20 x 1 + 18

20 = 18 × 1 + 2

18 = 2 × 9 +0

ইয়াত ভাগশেষ শূন্য হ’ল। গতিকে আমাৰ প্ৰণালীও বন্ধ হ’ব।

গতিকে 1848 আৰু 4058 ৰ গ.সা. উ 2.

2. দেখুওৱা যে যিকোনো যোগাত্মক অযুগ্ম অখণ্ড সংখাই 6q + 1, বা 6q + 3,

বা

6q+5 আৰ্হিৰ, য’ত q এটা কোনোবা অখণ্ড সংখ্যা।

সমাধান : ইউক্লিডৰ বিভাজন প্ৰমেয়িকা ব্যৱহাৰ কৰি আমি পাওঁ

a = bq + r ————–(i), r ≤ 0 < b

b = 6, (i) ত ব্যৱহাৰ কৰি আমি পাওঁ.

a = 6q + r [ 0 ≤ r<6 অর্থাৎ r=0,1,2,3,4,5]

যদি r= 0, a = 6q, 6q, 6 ৰে বিভাজা → 6q যুগ্ম

যদি r = 1, a = 6q + 1, 6q + 1, 2 ৰে বিভাজ্য নহয়

যদি r = 2, a = 6q + 2, 6q + 2, 2 ৰে বিভাজ্য হয় → 6q + 2 যুগ্ম

যদি r = 3, a = 6q + 3, 6q + 3, 2 ৰে বিভাজ্য নহয়

যদি r = 4, a = 6q + 4, 6q + 4, 2 ‘ৰে বিভাজ্য হয় → 6q + 4 যুগ্ম

যদি r = 5, a = 6q + 5, 6q + 5, 2 ৰে বিভাজ্য নহয়

6q, 6q +1, 6q + 2, 6q + 3,6g+ 4,69+5 সংখ্যাকেইটা যুগ্ম বা অযুগ্ম। কিন্তু 6q,

6q+2, 6q + 4 যুগ্ম

গতিকে, বাকী থকা 6q + 1,6q+3.6q+5 অযুগ্ম।

3. 616 সদস্যৰ এটা সৈন্যবাহিনীৰ গোটে 32 জনীয়া এটা সেনাদলৰ পিছে পিছে কদম-খোজ কাঢ়ি কাঢ়ি যাবলগীয়া হ’ল৷ দুয়োটা দলেই একে সমান সংখ্যক স্তম্ভত কদম-খোজ কাঢ়িবলগীয়া হ’ল৷ তেওঁলোকে খোজ কাঢ়িবলগীয়া স্তম্ভৰ উচ্চতম সংখ্যা কি হ’ব?

সমাধান : 616 আৰু 32 গ. সা. উ., সর্বোচ্চ স্তম্ভ হ’ব। এতিয়া আমি 616 আৰু 32 ৰ গ. সা. উ. উলিয়াব লাগে। 616 আৰু 32 ত ইউক্লিডৰ বিভাজন প্রমেয়িকা ব্যৱহাৰ কৰি

আমি পাওঁ, 616 = 32×19 +8

আকৌ, 32 আৰু 8 ত ইউক্লিডৰ বিভাজন প্রমেয়িকা ব্যৱহাৰ কৰি আমি পাওঁ,

32 = 8×4+O

যিহেতু ভাগশেষ শূন্য, গতিকে আমাৰ প্ৰক্ৰিয়াও বন্ধ হ’ব। গতিকে 616 আৰু 32 ৰ

গ. সা. উ. ৪

গতিকে মুঠ স্তম্ভৰ সংখ্যা ৪।

4. ইউক্লিডৰ বিভাজন প্ৰমেয়িকা ব্যৱহাৰ কৰি দেখুওৱা যে যিকোনো যোগাত্মক অখণ্ড সংখ্যাৰ বৰ্গই হয় 3m নাইবা 3m + 1 আৰ্হিৰ, য’ত m এটা কোনোবা অখণ্ড সংখ্যা। [ইংগিত: ধৰা x এটা যিকোনো যোগাত্মক অখণ্ড সংখ্যা। তেন্তে ইয়াৰ আৰ্হি হ’ব 3q, 3q + 1 বা 3q + 2 এতিয়া ইহঁতৰ প্ৰতিটোকে বৰ্গ কৰা আৰু দেখুওৱা যে সিহঁতক 3m বা 3m + 1 আৰ্হিত লিখিব পাৰি।]

সমাধান : ইউক্লিডৰ বিভাজন প্ৰমেয়িকা ব্যৱহাৰ কৰি আমি পাওঁ,

a=bq + r ————–→ (1)

b = 3, (1) ত বহুৱাই আমি পাওঁ,

a = 3q + r, [0 ≤ r <3, অর্থাৎ, r= 0,1,2]

যদি r = 0, a = 3q → a =9q ————–→ (2)

যদি r=1, a = 3q+1 → d =9q+6q +1 ————–→ (3)

যদি r =2, a = 3q+2 → a = 9q+12q + 4 ————–→ (4)

(2) ব পৰা 3m আৰ্হিৰ বৰ্গ 9q’ য’ত m =3q

(3) ৰ পৰা 9q2+6q +1 অর্থাৎ, 3(3q+2q) +1, 3m+1 ৰ আৰ্হিৰ বৰ্গ য’ত

m = 3q2+2q

(4) ৰ পৰা 9q±+12q + 4 অর্থাৎ, 3(3q+4q + 1)+1,3m +1 আৰ্হিৰ বৰ্গ, য’ত

m = 3q2+4q + 1

গতিকে, ধনাত্মক অখণ্ড সংখ্যাৰ বৰ্গ 3m বা 3m +1 আৰ্হিৰ, য’ত m এটা কোনো অখণ্ড সংখ্যা।

5. ইউক্লিডৰ বিভাজন প্রমেয়িকা ব্যৱহাৰ কৰি দেখুওৱা যে যি কোনো যোগাত্মক অখণ্ড সংখ্যাৰ ঘনফলটো 9m, 9m + 1 নাইবা 9m + 8 আৰ্হিৰ ৷

সমাধান : ধৰাহ’ল x এটা ধনাত্মক অখণ্ড সংখ্যা। তেতিয়া ই 3q বা 3q +1 বা 3q +2 আৰ্হিৰ।

চৰ্ত-I. যেতিয়া x = 3q এই ক্ষেত্ৰত আমি পাওঁ,

x³ = (3q)³ = 27q³ = 9 (3q³) = 9m, য’ত m = 3q³

চৰ্ত-II. যেতিয়া x = 3q + 1 এই ক্ষেত্ৰত আমি পাওঁ,

x³ = (3q+1)³ ⇒ x³ = 27q³ + 27q²+9q+1

→ x = 9(3q³ +9q² +q) + 1

→ x³=9m+1, য’ত m = (3q³+3q+q)

চৰ্ত-III. যেতিয়া x=3q +2 এই ক্ষেত্ৰত আমি পাওঁ,

x³ = (3q+2)³

→ x³ = 27q³ + 54q²+36q+8

→ x³= 9q (3q² +69+ 4) +8

→ x³ =9m+8, য’ত m = q (3q2 + 6q + 4)

গতিকে, x³ ,9m বা 9m+1 বা 9m+8 আৰ্হিৰ।

6. হিমাদ্রীয়ে 625 টা ভাৰতীয় আৰু 325 টা আন্তৰাষ্ট্ৰীয় ডাকটিকট সংগ্ৰহ কৰিলে। তাই এইবোৰ বিশেষ থূপত প্ৰদৰ্শন কৰিবলৈ বিচাৰে যাতে এটাও ডাক টিকট ৰৈ নাযায়। হিমাদ্রীয়ে সর্বাধিক কিমানটা থূপত ডাকটিকটবোৰ প্ৰদৰ্শন কৰিব পাৰিব?

সমাধান : 325 আৰু 625 ৰ গ. সা. উ সর্বাধিক থূপ হ’ব। এতিয়া আমি 326 আৰু 625 ৰ গ.সা. উ উলিয়াব লাগে

ইউক্লিডৰ বিভাজন প্ৰমেয়িকা ব্যৱহাৰ কৰি পাওঁ

300 = 25 × 12+0

625= 325 x 1+300

325 = 300 x1 +25

যিহেতু ভাগশেষ শূন্য, গতিকে আমাৰ প্ৰক্ৰিয়াও বন্ধ হ’ব।

গতিকে 325 আৰু 625 ৰ গ.সা.উ 25.

গতিকে ডাক টিকটৰ সৰ্বাধিক থুপ হ’ব 25 টা।

7. দুডাল ৰছীৰ দৈৰ্ঘ্য ক্ৰমে 64 ছে. মি. আৰু 80ছে. মি. । দুয়োডালৰ পৰা সমান দৈৰ্ঘ্যৰ টুকুৰা কাটি উলিয়াব লাগে। অকণো ৰৈ নোযোৱাকৈ দুয়োডাল ৰছীৰ পৰা কাটি উলিয়াৰ পৰা তেনে টুকুৰাৰ সৰ্বাধিক দৈর্ঘ্য কিমান হ’ব?

সমাধান : 64 আৰু 80 ৰ গ. সা. উ. হ’ব ৰছীৰ টুকুৰাৰ সৰ্বাধিক দৈৰ্ঘ্য।

এতিয়া আমি 64 আৰু 80 ৰ গ. সা.উ. উলিয়াব লাগে।

ইউক্লিডৰ বিভাজন প্ৰমেয়িকা ব্যৱহাৰ কৰি পাওঁ

80 = 64 × 1 + 16

64 = 16 x 4 +0

যিহেতু ভাগশেষ শূন্য গতিকে আমাৰ প্ৰক্ৰিয়াও বন্ধ হ’ব।

গতিকে 64 আৰু 80 গ.সা.উ হ’ব 16

.:. ৰছীৰ টুকুৰাৰ সৰ্বাধিক দৈৰ্ঘ্য হ’ব 16 ছে. মি.

অনুশীলনী- 1.2

1. প্ৰতিটো সংখ্যাকে ইয়াৰ মৌলিক উৎপাদকবোৰৰ গুণফল হিচাপে প্ৰকাশ কৰাঃ

(i) 140 (ii) 156 (iii) 3825 (iv) 5005 (v) 7429

সমাধানঃ (i) মৌলিক উৎপাদকৰ বাবে উৎপাদক বৃক্ষ প্ৰণালী ব্যৱহাৰ কৰি আমি পাওঁ,

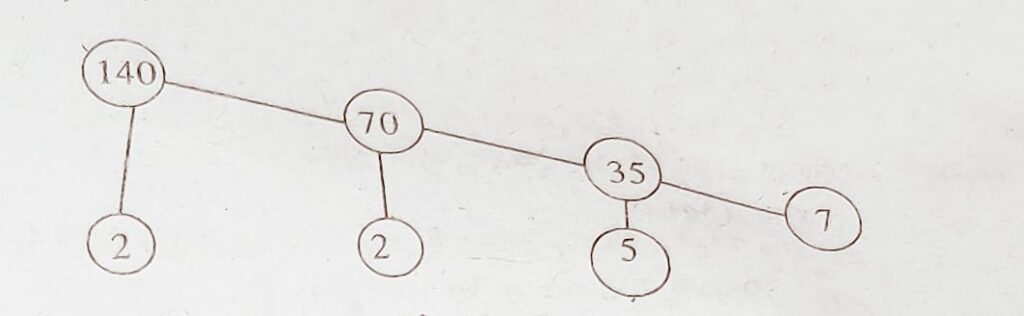
:. 140 = 2 x 2 × 5 ×7 = 22 × 5 × 7

সমাধান : (ii) মৌলিক উৎপাদকৰ বাবে উৎপাদক বৃক্ষ প্ৰণালী ব্যৱহাৰ কৰি আমি পাওঁ,

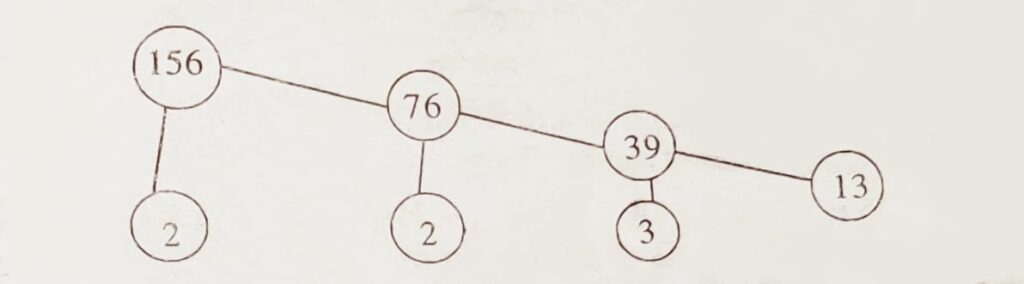
:. 156 = 2 x 2 x 3 x 13

সমাধানঃ (iii) মৌলিক উৎপাদকৰ বাবে উৎপাদক বৃক্ষ প্ৰণালী ব্যৱহাৰ কৰি আমি পাওঁ,

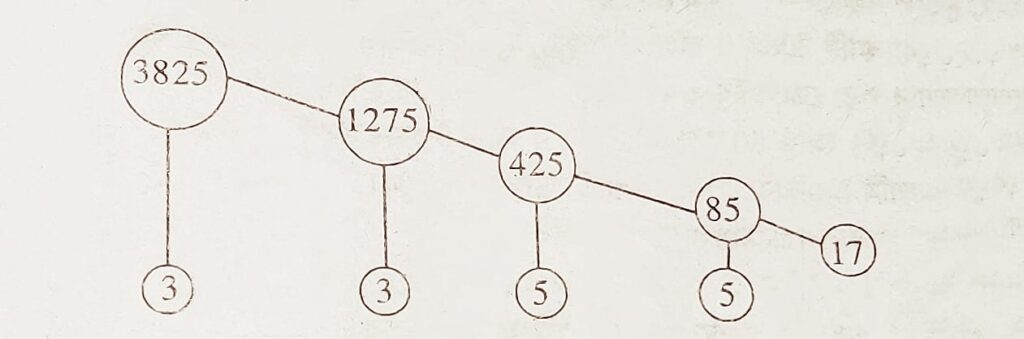
:. 3825 = 3 x 3 × 5 × 5 × 17

সমাধান : (iv) মৌলিক উৎপাদকৰ বাবে উৎপাদক বৃক্ষ প্রণালী ব্যৱহাৰ কৰি আমি পাওঁ,

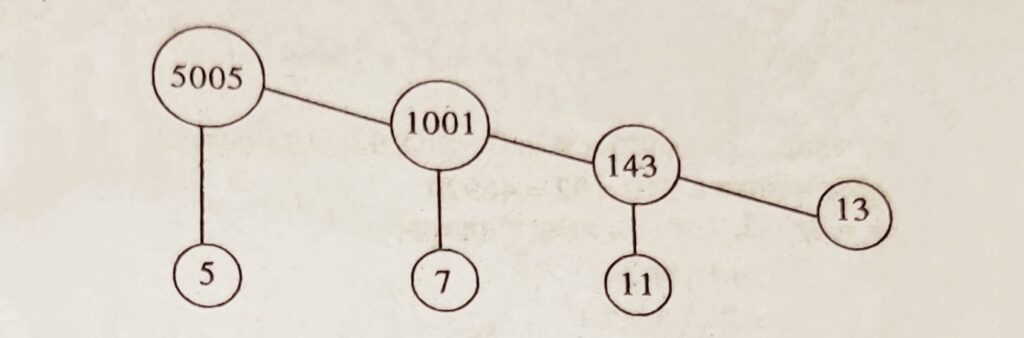
:. 5005 = 5 x 7×11×13

সমাধান : (v) মৌলিক উৎপাদকৰ বাবে উৎপাদক বৃক্ষ প্রণালী ব্যৱহাৰ কৰি আমি পাওঁ,

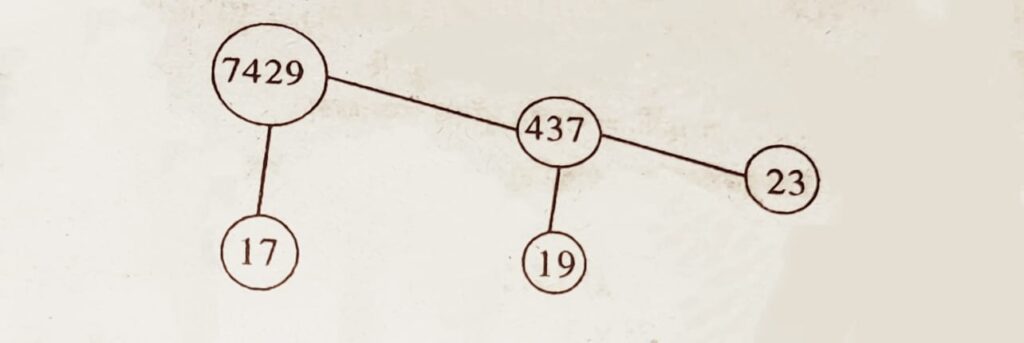
:. 7429 = 17 × 19 × 23

2. তলৰ অখণ্ড সংখ্যাকেইযোৰৰ ল.সা.গু. আৰু গ.সা.উ. উলিওৱা। সত্যাপন কৰা যে

ল.সা.গু. x গ.সা.উ. = সংখ্যাদুটাৰ গুণফল।

(i) 26 আৰু 91

(ii) 510 আৰু 92

(iii) 336 আৰু 54

সমাধান : (i) 26 আৰু 91

আমি পাওঁ, 26 = 2 × 13

91=7 x 13

গতিকে, ল.সা.গু (26,91) = 2 × 7 × 13 = 182

গ.সা.উ. (26, 91) = 13

এতিয়া, ল. সা.গু. (26, 91) × গ. সা. উ. (26, 91) = 182 × 13 = 2366

সংখ্যা দুটাৰ পূৰণফল = 26 × 91 = 2366

গতিকে, ল.সা.গু. × গ. সা. উ = সংখ্যা দুটাৰ পূৰণফল।

সমাধান : (ii) 510 আৰু 92

আমি পাওঁ, 510 = 2 x3⁵.

92= 2² x 23

:. (510, 92) = 2² x 35 x 23 =23460

গ.সা.উ. (510,92) = 2

এতিয়া, ল.সা.গু. (510,92) x গ.সা.উ. (510,92) = 23460 x 2 = 46920

সংখ্যাদুটাৰ পূৰ্ণফল = 510 x 92 = 46920

গতিকে, ল.সা.গু x গ.সা.উ. = সংখ্যা দুটাৰ পূৰণফল।

সমাধান : (iii) 336 আৰু 54

আমি পাওঁ, 336 = 2⁴ x 3 x 7

54= 2 x 3³

:. (336, 54) = 2⁴ x 3³ x 7= 3024

গ. সা.উ. (336, 92) = 2 x 3 = 6

এতিয়া, ল.সা.গু.(336,54) x গ.সা.উ. (336,54) = 3024× 6 = 18,144

সংখ্যাদুটাৰ পূৰণফল = 336 x 54 = 18 , 144

গতিকে, ল.সা.গু x গ.সা.উ. = সংখ্যা দুটাৰ পূৰণফল।

3. মৌলিক উৎপাদকীকৰণ পদ্ধতিৰে তলৰ অখণ্ড সংখ্যাবোৰৰ ল.সা.গু. আৰু গ.সা.উ. উলিওৱা।

(i) 12, 15 আৰু 21

(ii) 17, 23 আৰু 29

(iii) 8, 9 আৰু 25

সমাধান : (i) 12 = 22 x 3

15 = 3 x 5

আৰু 21 = 3 x 7

:. এই অখণ্ড সংখ্যাবোৰৰ গ.সা.উ. 3

12, 15 আৰু 21ৰ মৌলিক উৎপাদকৰ বৃহত্তম ঘাত 2², 3¹, 5¹ আৰু 7¹

গতিকে, ল.সা.গু. (12, 15, 21) = 2² x 3¹ x 5¹x7¹ = 420

সমাধান : (ii) 17, 23 আৰু 29

17, 23, 29 ৰ কোনো সাধাৰণ মৌলিক উৎপাদক নাই। গতিকে, গ.সা.উ. 1

17, 23, 29 ৰ ল.সা.গু = 17 × 23 x 29 = 11339

.:. গ.সা.উ. (17, 23, 29)=1

ল.সা.গু. (17, 23, 29) = 11339

সমাধান : (iii) 8, 9 আৰু 25

8 = 2 x 2 x 2 = 2³

9=3³

25 = 5²

গ.সা.উ. (8, 9, 25) = 1 [ 8,9,25 ৰ সাধাৰণ উৎপাদক নাই।

:. ল.সা.গু= 2³ x 32 x 5² =1800

4. দিয়া আছে গ.সা.উ. (306,657) = 91 ল.সা.গু. (306,657) উলিওৱা

সমাধানঃ

আমি পাওঁ

গ.সা.উ. (306,657) = 9

আমি জানো যে, ল.সা.গু x গ.সা.উ = সংখ্যা দুটাৰ পূৰণফল

→ ল.সা.গু x 9 = 306×657

→ ল.সা.গু = (306 × 657) / 9 = 22338

গতিকে, ল.সা.গু (306,657) = 22338

5. পৰীক্ষা কৰা, কোনোবা স্বাভাৱিক সংখ্যা 71i অৰ ক্ষেত্ৰত 6” সংখ্যাটো 0 অংকেৰে শেষ হ’ব পাৰেনে নাই।

সমাধানঃ n ৰ কোনো মানৰ ক্ষেত্ৰত যদি 6ⁿ সংখ্যাটো শূন্য অংকটোৰে শেষ হ’বলগীয়া হয়, তেন্তে ই 5 ৰে বিভাজ্য হ’ব।

কিন্তু আমি জানো যে, 6ⁿ ৰ মৌলিক উৎপাদক 2 আৰু 3

আকৌ, পাটীগণিত মৌলিক উপপাদ্যই নিশ্চিত কৰে যে 6ⁿ অইন কোনো মৌলিক উৎপাদক নাই।

গতিকে, এনে কোনো স্বাভাৱিক সংখ্যা n নাই যাৰ ক্ষেত্ৰত 6ⁿ শূন্য অংকৰে শেষ হয়।

6. 7 × 11 × 13 + 13 আৰু 7× 6 ×5 × 4 × 3 × 2×1+5 সংখ্যা দুটা কিয় যৌগিক সংখ্যা, ব্যাখ্যা কৰা।

সমাধানঃ আমি জানো যে, 7×11×13 + 13 = 1001 + 13 = 1014

1014 = 2 x 3x13x13

গতিকে ই মৌলিক উৎপাদক, 2 × 3 × 13 × 13 ৰ পূৰণফল

গতিকে, এইটো এটা যৌগিক সংখ্যা।

7× 6 × 5 × 4 × 3 × 2 × 1+ 5 = 5040 + 5 = 5045

5045 = 5 x 1009

গতিকে, ই মৌলিক উৎপাদক, 5 × 1009 ৰ পূৰণফল ৷

গতিকে, ই এটা যৌগিক সংখ্যা।

7. এখন খেল পথাৰৰ চাৰিওপিনে এটা বৃত্তাকাৰ পথ। খেল পথাৰখন গাড়ীৰে এবাৰ ঘূৰিবলৈ ছোনিয়াৰ 18 মিনিট লাগে, য’ত একেটা ঘূৰণতে ৰবিৰ লাগে 12 মিনিট। ধৱা তেওঁলোকে একেটা বিন্দুতে একে সময়তে আৰু একেটা দিশত যাত্রা আৰম্ভ কৰে। কিমান মিনিট পিছত তেওঁলোক আকৌ আৰম্ভণিৰ বিন্দুটোত লগ লাগিব ?

সমাধানঃ 18 আৰু 12 ৰ ল.সা.গু হ’ব উলিয়াব লগা সময়।

আমি পাওঁ, 18 = 2 x 3²

12 = 2² x 3

18 আৰু 12 ৰ ল.সা.গু = 2² x 3² = 36

গতিকে, 36 মিনিট পিছত ৰবি আৰু ছোনিয়াই আকৌ আৰম্ভণি বিন্দুত লগ লাগিব।

8 (i) এটা ৰেজিমেণ্টত থকা সৈনিকবোৰক 15, 20 বা 25 জনকৈ লৈ কিছুমান শাৰীত থিয় কৰাব পাৰি। ৰেজিমেণ্টটোত অতি কমেও কিমানজন সৈনিক আছে?

সমাধানঃ ৰেজিমেণ্টটোত অতিকমেও থকা সৈনিকৰ সংখ্যা = ল.সা.গু (15, 20, 25 )

এতিয়া,

15 = 3 x 5

20 = 2² x 5

25 = 5²

:. (15, 20, 25) = (3×2²x5²)

= 3x 4 x 25

= 300

.:. ৰেজিমেণ্টত অতি কমেও 300 জন সৈনিক আছে।

(ii) এটা ঘণ্টা 18 ছেকেণ্ড আৰু আন এটা ঘণ্টা 60 ছেকেণ্ডৰ অন্তৰালত বাজে। কোনো এক সময়ত দুয়োটা ঘণ্টা একেলগে বাজিলে তাৰ কিমান ছেকেণ্ড পিছত ঘণ্টাদুটা পুনৰ একেলগে বাজিব? [HSLC 2022]

সমাধানঃ উলিয়াব লগা ছেকেণ্ড = ল. সা. গু (18, 60)

এতিয়া, 18 = 2×3²

60 = 2² x 3 x 5

:. ল. সা. গু (18,60) = (3² x 2²×5)

= (9 × 4 x 5)

= 180

গতিকে 180 ছেকেণ্ডৰ পিছত ঘণ্টা দুটা একেলগে বাজিব।

(iii) এটা অনাতাঁৰ কেন্দ্ৰই প্ৰতি দুদিনৰ মূৰে মূৰে ‘অসম সংগীত’ টো বজায় । আন এটা কেন্দ্ৰই একেটা সংগীত প্রতি তিনি দিনৰ মূৰে মূৰে বজায়। 30 দিনত মুঠতে কিমানবাৰ দুয়োটা অনাতাঁৰ কেন্দ্ৰই একেটা দিনত সংগীতটো বজাব ?

সমাধানঃ এটা অনাতাঁৰ কেন্দ্ৰই অসম সঙ্গীত বজায় 2 দিনৰ মূৰে মূৰে

আন এটা অনাতাঁৰ কেন্দ্ৰই অসম সঙ্গীত বজায় 2 দিনৰ মূৰে মূৰে

.: 30 দিনত মুঠতে দুয়োটাৰ অনাতাঁৰ কেন্দ্ৰই একেটা দিনত সংগীতটো বজাব = 30 / 60 = 5 বাৰ।

অনুশীলনী- 1.3

1. দেখুওৱা যে √5 অপৰিমেয়।

সমাধানঃ ধৰাহ’ল √5 এটা পৰিমেয় সংখ্যা।

তেতিয়া, √5 ক p/q আকাৰত প্ৰকাশ কৰিব পাৰি। য’ত p আৰু q দুটা অখণ্ড সংখ্যা, যাৰ 1 ৰ বাহিৰে কোনো সাধাৰণ উৎপাদক নাই। q ≠ 0.

√5= p/q => 5 = p²/q² => p² = 5q² ——————→(1)

⇒ p², 5 ৰে বিভাজ্য হয়।

⇒p, 5 ৰে বিভাজ্য —————–→ (2)

ধৰা হ’ল, p = 5m ⇒ p² = 25m²

p²ৰ মান (1) ত বহুৱাই আমি পাওঁ, 25m² = 5q ⇒ 5m² = q²

⇒ q², 5 ৰে বিভাজ্য হয় ⇒ q, 5 ৰে বিভাজ্য হয় ———————→ (3)

(2) ৰ পৰা p, 5 ৰে বিভাজ্য হয় আৰু (3) ৰ পৰা পাওঁ, q, 5 ৰে বিভাজ্য হয় ।

ইয়াৰ অৰ্থ p আৰু q, 5 ৰে বিভাজ্য হয়। কিন্তু ‘p আৰু q ৰ 1ৰ বাহিৰে মৌলিক উৎপাদক নাই’ এই সত্যটোক বিৰোধ কৰে। এই বিৰোধৰ কাৰণ এয়ে যে √5 পৰিমেয় বুলি কৰা ধাৰ্যটো অশুদ্ধ।

গতিকে, √5 এটা অপৰিমেয় সংখ্যা।

2. দেখুওৱা যে 3 + 2√5 অপৰিমেয়। [HSLC 2016, 2022]

সমাধানঃ বিৰুদ্ধভাৱে ধৰো যে 3 + 2√5 পৰিমেয়।

তেন্তে ,

আমি a আৰু b ৰ (b≠0) সহ মৌলিক দুটা পাব পাৰো যাতে

3+2√5 = a/b ⇒ 2 √5 = a/b – 3 ⇒ √5 = (a-3b) /2b

⇒ √5 পৰিমেয় [ :: a,b, অখণ্ড সংখ্যা :.(a-3b) /2b পৰিমেয় সংখ্যা]

গতিকে, √5 অপৰিমেয়’ এই সত্যতাৰ বিৰোধ কৰে। এই বিৰুদ্ধৰ কাৰণ হ’ল যে আমাৰ ধার্য 3 + 2 √5 পৰিমেয়।

গতিকে, 3+2√5 অপৰিমেয়।

3. দেখুওৱা যে তলৰ সংখ্যাবোৰ অপৰিমেয় :

(i) ¹/_√2

(ii) 7√5

(iii) 6 + √2

সমাধান : (i) বিৰুদ্ধভাৱে আমি ধৰো ¹/_√2 এই পৰিমেয়।

সেয়ে আমি a আৰু b (b ≠0) ব সহ মৌলিক পাব পাৰো যে = ¹/_√2 = ^a/_b ———–(1)

কিন্তু, a আৰু b অশূন্য অখণ্ড সংখ্যা।

:. ^a/_b পৰিমেয়।

(1) ৰ পৰা আমি পাওঁ, অপৰিমেয় সংখ্যা।

কিন্তু ই সত্যতাৰ বিৰোধ কৰে যে ¹/_√2 এটা পৰিমেয় সংখ্যা।

গতিকে, ¹/_√2 এটা পৰিমেয় সংখ্যা।

সমাধান : (ii) যদি সম্ভৱ ধৰা হ’ল 7 √5 পৰিমেয়।

গতিকে, ইয়াৰ সৰল আকাৰ 7 √5 = ^a/_b

তেতিয়া, a আৰু b দুটা অশূন্য অখণ্ড সংখ্যা যাৰ 1 ৰ বাহিৰে আন কোনো মৌলিক উৎপাদক নাই।

এতিয়া, 7 √5 = ^a/_b ⇒ √5 = ^a/_7b ———–(1)

কিন্তু a আৰু 7b দুটা অশূন্য অখণ্ড সংখ্যা।

:. ^a/_7b পৰিমেয়।

গতিকে, (i) ৰ পৰা আমি পাওঁ, √5 এটা পৰিমেয়।

‘√5 অপৰিমেয়’ এই সত্যতাৰ বিৰোধ কৰে।

বিৰুদ্ধ ফল ওলোৱাৰ কাৰণ আমি ধৰিছো যে 7 √5 পৰিমেয়।

গতিকে, 7√5 পৰিমেয়।

সমাধান : (iii) ধৰাহ’ল, 6+√2 পৰিমেয় সংখ্যা যাতে 6+√2 = 6. য’ত a আৰু b দুটা সহ মৌলিক সংখ্যা। তেতিয়া

6+√2 = ^a/_b ⇒ √2 = ^a/_b – 6 ⇒ √2 ^a-6b/_b ⇒ √2 পৰিমেয় ই নীতি বিৰুদ্ধ।

গতিকে, 6 + √2 অপৰিমেয়।

অনুশীলনী- 1.4

1. দীৰ্ঘ হৰণ নকৰাকৈ তলত উল্লেখ কৰা পৰিমেয় সংখ্যাবোৰৰ কোনবোৰৰ দশমিক বিস্তৃতি পৰিসমাপ্তি (সাবধি) নাইবা কোনবোৰৰ নিৰবধি পৌনঃপুনিক দশমিক বিস্তৃতি থাকিব বর্ণনা কৰা :

(i) ¹³/₃₁₂₅ (ii) ¹⁷/₈ (iii) ⁶⁴/₄₅₅ (iv)¹⁵/₁₆₀₀ (v) ²⁹/₃₄₃

(vi) ²³/_2³5² (vii) ¹²⁹/_2²5⁷7⁵ (viii) ⁶/₁₅ (ix) ³⁵/₅₀ (x) ²⁷/₂₁₀

সমাধান : (i) 3125 ৰ হৰ 2⁰x5⁵ আকাৰৰ। গতিকে ¹³/₃₁₂₅ পৰিসমাপ্ত (সাৱধি)।

(ii) যিহেতু ৪ ৰ হৰ 2⁰x5⁵ আকাৰৰ। গতিকে 17/8 পৰিসমাপ্ত (সাৱধি)।

(iii) যিহেতু 455 ৰ হৰ 2ⁿx5^m আকাৰৰ নহয়, গতিকে ⁶⁴/₄₅₅ নিৰৱধি পৌনঃপুণিক।

(iv) যিহেতু 1600 ৰ হৰ 2⁶x5² আকাৰৰ, গতিকে ¹⁵/₁₆₀₀ পৰিসমাপ্ত (সাৱধি)।

(v) যিহেতু 343 ৰ হৰ 2ⁿx5^m আকাৰৰ নহয়, গতিকে ²⁹/₃₄₃ নিৰৱধি পৌনঃপুণিক।

(vi) যিহেতু হৰ 2³x5² আকাৰৰ, গতিকে ²³/_{2³ ×5²} পৰিসমাপ্ত (সাৱধি)।

(vii) যিহেতু হৰ 2²5⁷7⁵, 2ⁿx5^m আকাৰৰ নহয়, গতিকে ^129/_2²5⁷7⁵ নিৰৱধি পৌনঃপুণিক।

(viii) ¹⁶/₅ = ²/₅ ইয়াত হৰ 5 , 2⁰x5¹ আকাৰৰ, গতিকে ¹⁶/₅ পৰিসমাপ্ত (সাৱধি)।

(ix) যিহেতু হৰ 50, 2¹x5² আকাৰৰ, গতিকে ³⁵/₅₀ পৰিসমাপ্ত (সাৱধি)।

(x) যিহেতু হৰ 210, 2ⁿx5^m আকাৰৰ নহয়, গতিকে, ⁷⁷/₂₁₀ নিৰৱধি পৌনঃপুণিক।

2. ওপৰৰ প্ৰশ্ন-1 অত যিবোৰ পৰিমেয় সংখ্যাৰ পৰিসমাপ্ত দশমিক বিস্তৃতি আছে সেইবোৰৰ দশমিক বিস্তৃতিবোৰ লিখি দেখুওৱা

সমাধান : (i)¹³/₃₁₂₅ = ¹³/_5² = ^{25 x13}/_{2⁵ x5⁵} = ⁴¹⁶/_10⁵ = 0.00416

(ii) ¹⁷/₈ =¹⁷/_2³ = ²¹²⁵/₁₀₀₀ = 2.125

(iv) ¹⁵/₁₆₀₀ = ^{3 X 5}/_{2⁶ X 5²} = 3 x 5 x 5⁴/₁₀₀₀ = 3 X 5⁴/_10⁶ = 0.009375

(vi) ²³/_2³x5² =^{23 X 5}/_10³ =¹¹⁵/₁₀₀₀ = 0.115

(vii) ⁶/₁₅ = ^{2 X 2}/_{2 X 5} = ⁴/₁₀ = 0.4

(ix) ³⁵/₅₀ = ⁷/₁₀ = 0.7

3. তলৰ বাস্তৱ সংখ্যাবোৰৰ ইয়াত দেখুওৱা ধৰণে দশমিক বিস্তৃতি আছে। প্ৰতিটোৰ ক্ষেত্ৰতে ই এটা পৰিমেয় হয় নে নহয় সিদ্ধান্ত কৰা। যদি ই পৰিমেয় আৰু ই ^p/_q আৰ্হিৰ, তেন্তে ইয়াৰ q ৰ মৌলিক উৎপাদকীকৰণৰ বিষয়ে কি ক’ব পাৰিবা?

সমাধান : (i) পৰিমেয় q = 10⁹ = 2⁹ x 5⁹

(ii) পৰিমেয় নহয়।

(iii) পৰিমেয়, q ৰ মৌলিক উৎপাদকৰো 2 বা 5 ৰ বাহিৰে অন্য এটা উৎপাদক থাকিব।

বিকল্পধর্মী প্রশ্নোত্তৰ

1. ইউক্লিডৰ বিভাজন a আৰু b দুটা যোগাত্মক অখণ্ড সংখ্যা দিয়া থাকিলে এ আৰু । এনে দুটা পূৰ্ণ সংখ্যা বিচাৰি পোৱা যাব যাতে a = bq + r, য’ত rয়ে সিদ্ধ কৰিব ? [HSLC 2016]

(a) 1 < r < b (b) o <r <b (c) o ≤ r < b (d) o < r ≤ b

সমাধানঃ (c) 0 ≤ r < b

2. ⁴³ / _2⁴x5³ পৰিমেয় সংখ্যাটিৰ দশমিক প্ৰসাৰণৰ দশমিক স্থানৰ পৰিসমাপ্তি হোৱা স্থানৰ সংখ্যা হ’ল-

[HSLC 2017]

(a) 3 (b) 4 (c) 1 (d) 5

সমাধানঃ (b) 4

2. তলৰ বাস্তৱ সংখ্যাবোৰৰ কোনটো নিৰৱধি পৌনঃপুনিক হ’ব? [HSLC 2015]

(a) √3 (b) π (c) ¹/₇ (d) ¹³/₁₂₅

সমাধানঃ (c) ¹/₇

3. যদি ল.সা.গু (91, 26) = 182, তেতিয়া গ.সা.উ (91,26) = [HSLC 2016]

(a) 13 (b) 26 (c) 7 (d) 9

উত্তৰঃ (a) 13

4. আটাইতকৈ সৰু যিটো সংখ্যাৰে, √27 ক পূৰ্ণ কৰিলে এটা পৰিমেয় সংখ্যা পোৱা যাব, সেই সংখ্যাটো হ’ল : [HSLC 2017]

(a) √27 (b) 3√3 (c) √3 (d) 3

সমাধানঃ (c) √3

5. পৰিমেয় সংখ্যা ¹⁴⁵⁸⁸/₆₂₅ দশমিক প্ৰসাৰণ তলৰ কোনটো দশমিক স্থানৰ পিছত শেষ হ’ব?

[HSLC 2018]

(a) 2 (b) 3 (c) 4 (d) 5

সমাধানঃ (c) 4

6. তলৰ কোনটো পৰিমেয় সংখ্যা? [HSLC 2018]

(a) ^√2/_√3 (b) ^√2/_π (c) ^√5/_√6 (d) ^√3/_√27

সমাধানঃ (d) ^√3/_√27

7. তলৰ কোনটো নিৰবধি পৌনঃপুনিক দশমিক? [HSLC 2019]

(a) ³/₈ (b) ⁷/₈₀ (c) ⁶⁴/₄₅₅ (d)¹²⁴/₆₂₅

সমাধানঃ (c) ⁶⁴/₄₅₅

8. তলৰ কোনটোসংখ্যা অপৰিমেয়? [HSLC 2020]

(a) 0.14285714285714285 (b) ²²/₇ (c) π (d) ^√4/₁₁

সমাধানঃ (c) π

অতিৰিক্ত প্রশ্নোত্তৰ

1. প্ৰমাণ কৰা যে √2 এটা অপৰিমেয়। [HSLC 2019]

সমাধানঃ ধৰি লওঁ যে √2 এটা পৰিমেয় সংখ্যা।

:. √2= ^a/_b, য’ত a আৰু b সহমৌলিক। গতিকে b√2 = a

দুয়োপিনে বৰ্গ কৰি সজাই 2b² = a² (1)। গতিকে 2 য়ে a³ ক হৰণ কৰে। সেয়ে আমি লিখিব পাৰোঁ a = 2c, কোনোবা অখণ্ড cৰ ক্ষেত্ৰত। (1) ত ব মান বহুৱাই আমি পাওঁ, 2b² = 4c², অর্থাৎ b² = 2c² ইয়াৰ অৰ্থ হ’ল 2 য়ে b² ক হৰণ কৰে আৰু সেয়ে 2 য়ে b ক হৰণ কৰে।

গতিকে, a আৰু b উভয়ৰে অন্ততঃ এটা সাধাৰণ উৎপাদক আছে, যি 2। কিন্তু ইয়ে আমি ধৰা ‘a আৰু bৰ1 ৰ বাহিৰে অইন সাধাৰণ উৎপাদক নাই’ এই সত্যটোক বিবোধ কৰে। এই বিৰুদ্ধৰ কাৰণ এয়ে যে—’√2 পৰিমেয়’ বুলি কৰা আমাৰ ধাৰ্যটো অশুদ্ধ। সেয়ে আমি সিদ্ধান্তত উপনীত হ’লো যে √2 পৰিমেয়।

2. মৌলিক উৎপাদকীকৰণ পদ্ধতিৰে 96 আৰু 404 ৰ গ. সা. গু. উলিওৱা । ইয়াৰ পৰা সিহঁতৰ ল. সা. গু উলিওৱা। [HSLC 2019]

সমাধানঃ

96 = 2⁵ x 3,

404 = 2² x 101

গতিকে এই অখণ্ড সংখ্যা দুটাৰ গ.সা.উ. হ’ব 22 = 4

3. মৌলিক উৎপাদকীকৰণ পদ্ধতিৰে 6, 72, 120, ৰ গ. সা. উ. আৰু ল. সা. গু উলিওৱা। সংখ্যাকেইটাৰ পূৰণফল, গ. সা. উ আৰু ল.সা.গু.ৰ পূৰ্ণফল সমান হয়নে? [HSLC 2019]

সমাধানঃ 6 = 2 x 3 72= 23 x 3²

120 = 23 x 3 x 5

গ. সা. উ. (6, 72, 120) = 2¹ x 3¹= 2×3=6

ল. সা. গু (6, 72, 120) = 2³ x 3² x 5¹ = 360

4. 210 আৰু 55 ৰ গ. সা. উ.ক 210×5+55y আৰ্হিত প্ৰকাশ কৰিব পাৰি তেন্তে y নিৰ্ণয় কৰা।”

[HSLC 2017]

সমাধানঃ 210 আৰু 55 ত ইউক্লিডৰ বিভাজন প্ৰমেয়িকা ব্যৱহাৰ কৰি আমি পাওঁ

210 = 55 x 3+ 45. ————(i)

যিহেতু ভাগশেষ 45 = 0, গতিকে আমি 55 আৰু 45 ৰ ওপৰত বিভাজন প্রমেয়িকা প্ৰয়োগ কৰি পাওঁ, 55 = 45×1 + 10 ————(ii)

এতিয়া 45 আৰু 10 ৰ ওপৰত বিভাজন প্রমেয়িকা প্রয়োগ কৰি পাওঁ

45 = 4 x 10 +5

(iii) 10 আৰু 5 ৰ ওপৰত বিভাজন প্ৰমেয়িকা প্ৰয়োগ কৰি পাওঁ

10 = 5×2+0

(iv) এতিয়া ভাগশেষ শূন্য হ’ল। গতিকে আমাৰ প্ৰণালীও বন্ধ হ’ব। যিহেতু এই পৰ্যায়ত ভাজক 5, গতিকে 210 আৰু 55 ৰ গ. সা. উ. 5

:. 5=210×5 +55y ⇒ 55y = 5-210×5=5-1050

⇒ 55y = 1045 ⇒ y = ^-1045/₅₅ = -19

5. দেখুওৱা যে যিকোনো ধনাত্মক অযুগ্ম সংখ্যা 4q+1 বা 4g + 3 আৰ্হিৰ, য’ত g অখণ্ড সংখ্যা।

[H.S.L.C 2015]

সমাধানঃ ধৰাহ’ল ৫ ধনাত্মক অযুগ্ম সংখ্যা আৰু b = 4 বিভাজন প্রমেয়িকাৰ দ্বাৰা q আৰু স্থিত হয়, য’ত a = 4q + r, য’ত ০ ≤r<4

⇒ a = 4q বা a = 4g+1 বা a = 4q + 2

বা a = 4q+3[:. 0<r< 4 ⇒ r= 0, 1, 2, 3]

⇒ a = 4q + 1 বা a = 4q + 3 [:. a অযুগ্ম অখণ্ড সংখ্যা a ≠ 4q, a ≠ 4q+2]

গতিকে, যিকোনো ধনাত্মক অযুগ্ম সংখ্যা 4q+1 বা 4q + 3 আৰ্হিৰ, য’ত q অখণ্ড সংখ্যা।

6. প্রমাণ কৰা যে 3√2 অপৰিমেয়। [HSLC 2018]

সমাধানঃ বিৰুদ্ধভাৱে আমি ধৰো, 3 √2 পৰিমেয়।

সেয়ে আমি a আৰু b(b ≠0) সহমৌলিকযোৰ পাব পাৰো যে 3,√2 = ^a/_b। সজাই পাওঁ √2 = ^a/_3b। যিহেতু 3, a আৰু b বোৰ অখণ্ড, ^a/_3b পৰিমেয় আৰু সেয়ে √2 পৰিমেয়।

কিন্তু ইয়ে ‘√2 পৰিমেয়’ এই সত্যতাৰ বিৰোধ কৰে। গতিকে আমি সিদ্ধান্ত পালো যে 3√2 অপৰিমেয়।

৪. প্রমাণ কৰা যে √7 অপৰিমেয়। [HSLC 2020]

সমাধানঃ ধৰাহ’ল √7 এটা পৰিমেয় সংখ্যা।

তেতিয়া √7 ক ^p/_q আকাৰত প্ৰকাশ কৰিব পাৰি য’ত p আৰু q (q ≠0)

দুটা অখণ্ড সংখ্যা, যাৰ 1 ৰ বাহিৰে কোনো সাধাৰণ উৎপাদক নাই।

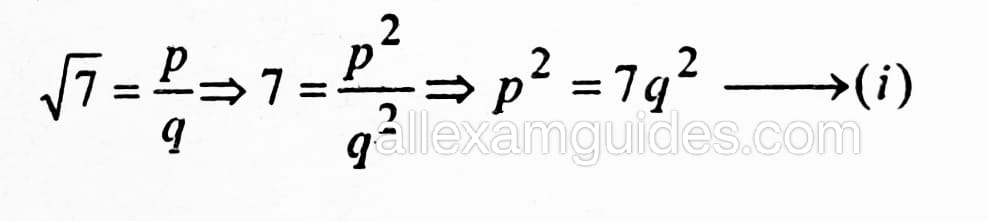
⇒ p², 7 ৰে বিভাজ্য হয়।

⇒ p, 7 ৰে বিভাজ্য হয়। ————–→ (2)

ধৰাহ’ল, p = 7m ⇒ p² = 49m²

p²ৰ মান (1)ত বহুৱাই আমি পাওঁ, 49m² = 7q² ⇒ 7m² = q²

⇒ q²,7 ৰে বিভাজ্য হয়, ⇒q, 7 ৰে বিভাজ্য হয় —————→ (3)

(2) ৰ পৰা p, 7 ৰে বিভাজ্য হয় আৰু (3) ৰ পৰা পাওঁ, q, 7 ৰে বিভাজ্য হয়।

ইয়াৰ অৰ্থ p আৰু q, 7 ৰে বিভাজ্য হয়। কিন্তু ‘p আৰু q’ ৰ 1 ৰ বাহিৰে মৌলিক উৎপাদক নাই’ এই সত্যটোক বিৰোধ কৰে। এই বিৰোধৰ কাৰণে এয়ে যে √7 পৰিমেয় বুলি কৰা ধাৰ্যটো অশুদ্ধ।

গতিকে √7 এটা অপৰিমেয় সংখ্যা।

Conclusion:

আমি বিশ্বাস কৰোঁ যে এই টোকাবোৰে শিক্ষাৰ্থীসকলক বিষয়বোৰৰ বিষয়ে ভালদৰে বুজাবুজি বিকশিত কৰাত আৰু তেওঁলোকৰ পৰীক্ষাৰ বাবে তেওঁলোকৰ আত্মবিশ্বাস বৃদ্ধি কৰাত সহায় কৰিব।

আমি নিশ্চিত যে এই টোকাবোৰে শিক্ষাৰ্থীসকলক তেওঁলোকৰ লক্ষ্য প্ৰাপ্ত কৰাত আৰু তেওঁলোকৰ শৈক্ষিক প্ৰদৰ্শন বৃদ্ধি কৰাত সহায় কৰিব। যদি আপুনি এই সমাধান সমূহ ভাল পায় আৰু সহায়ক হয় তেন্তে আপোনাৰ বন্ধুবৰ্গৰ সৈতে Share কৰিবলৈ নাপাহৰিব।